부동 소수점 2진수 표현에 대해서 작성을 합니다
2가지의 방법이 있습니다
64bias 와 127bias 표현법이 있습니다
주로 64 bias 를 사용하며 가끔씩 127bias 가 나타나기도 합니다
컴퓨터는 숫자 0과 1을 이용해서 숫자를 표현하는데, 부동소수점 (floating point) 방식은 숫자를 0과 1을 이용해서 (근사해서) 표현하는 방식 중 하나입니다.
부동소수점에서 부동은 움직이지 않는다는 뜻의 不動이 아니라, 오히려 그 반대의 의미로 소수점이 떠다니며 움직인다는 의미의 부동 (浮動)입니다.
이 페이지에서는 IEEE 754 표준 방식으로 숫자를 부동소수점으로 표현하는 방법에 대해 소개합니다.
(IEEE 754는 전기 전자 기술자 협회 (IEEE)에서 개발한 표준 부동소수점 방식이며 현재 컴퓨터에서 가장 널리 쓰이는 방식입니다.)
부동 소수점의 순서입니다
부호, 지수, 가수
IEEE 754 부동소수점 표현에서 숫자는 아래와 같이 부호부, 지수부, 가수부의 세 부분으로 구성됩니다.
각 부분의 역할과 사용하는 비트 수는 아래와 같습니다.
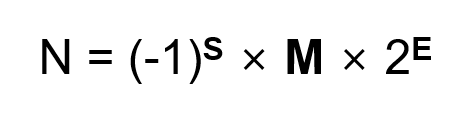
- 부호부 (Sign) : 1비트. 숫자의 부호를 나타내며, 양수일 때 0, 음수일 때1이 됩니다.
- 지수부 (Exponent) :8비트. 지수를 나타냅니다.
- 가수부 (Mantissa) : 23비트. 가수 또는 유효숫자를 나타냅니다.

32비트 단정도 (single precision) 부동소수점 표현.
위의 그림과 같이 숫자를 표현하고 저장하기 위해 32비트 (4바이트)를 사용하는 방식을 단정도 (single precision)라고 합니다.
배정도 (double precision) 표현에서는 64비트 (8바이트)를 사용합니다.
- 10진수를 2진수로 변환
- 정규화
- 지수계산
10진수를 2진수로 변환 합시다 ex) 128.5 를 2진법으로 전환해보겠습니다. => 10000000.1
정규화
흔한 64 bias 부터 해보겠습니다.
가수 부분이 0.1 이상이고 1보다 작게 소수점의 위치를 조정하여 지수부와 가수부를 분리합니다
10000000.1 => 0.100000001 *2^8
가수부 지수부
지수 계산
64bias의 2진법변환을 합니다 =>1000000 그리고 2^n 2의 n승의 수 8을 더합니다 8을 2진법으로 변경 1000
1000000
+ 1000
--------------
1001000 지수쪽 계산이 완료 되었으면 대입을 합시다. 64+8=72 를 2진법으로 변경해서 작성하셔도 상관없습니다.
0 100100010000000100000000~~
부호비트,지수부,가수부 순서대로 적어줍니다 그리고 나머지는 0으로 채워줍니다.
127bias 도 거의 비슷합니다
똑같은 128.5라고 생각하겠습니다
10000000.1 정규화 방법이 살짝 다릅니다 64bias는 0.1~0.9까지였다면 127bias 는 가수 부분이 1.xxxxxx로 표현되며 1은 항상 고정이므로 표현하지않습니다
10000000.1 => 1.00000001 *2^7
가수부 지수부
2의 n승의 숫자가 1줄어 들었고 0.~ 기준이 1.~ 으로 변경 되었습니다.
지수부 계산은 똑같습니다
127를 2진법으로 변경 => 01111111
+ 111
---------------
10000110 => 127+7 134 를 2진법으로 변경
앞에 1. < 이것은 제외 하고 표현 합니다 그후 똑같습니다
01000011000000001 ( 나머지 0으로 표시 )
(부호비트),(지수부),(가수부)

참고 자료 https://codetorial.net/articles/floating_point.html
'CS > 컴퓨터구조' 카테고리의 다른 글
| 중앙 처리장치(CPU) (0) | 2023.11.10 |
|---|---|
| 정수의 산술 연산 (1) | 2023.11.03 |
| 음수의 표현 (0) | 2023.10.28 |
| 진법 변환 (0) | 2023.10.19 |
| 컴퓨터 시스템의 개요(컴퓨터 5대 장치포함.) (1) | 2023.10.19 |


