가,감산의 기본 기법
연산장치 내에서의 가산 또는 감산에 있어서 정, 부의 2진수 취급 방법을 살펴봐야 합니다. 수는 정(+) 또는 부(-) 의 어느한쪽이며
계산기에 기억된 데이터는 0또는 비트중에 어느 한 가지를 나타내고 있으므로 수의 부호는 0 또는 1로서 기억됩니다.
예를 들면 0으로 양의 수를 나타내면 1로 음의 수를 나타내게 됩니다. 만약 16비트의 수를 사용하면 1비트는 항상 부호 비트로서 읽혀지고 남은 15비트가 수치의 크기를 나타내고 있습니다.

두 개의 부호가 같은지 다른지 조사하기 위해서 우선 부호를 비교할 필요가 있게 됩니다. 그리고 서로 다른 부호라고 한다면 A-B 와 B-A 의 양쪽 형태를 만들어 그 결과에 답의 부호를 결정하는 데 어느 것이 맞는가 알아 볼 필요가 있습니다. 특히 보수 기법에서는 2의 보수가 실제의 고속 연산으로 자주 사용됩니다.

가산
2진수 연산의 기본은 가산이며 가산은 가수와 파가수의 하위 비트의 자리올림 사이에서 이루어 지며 합과 자리올림이 얻어집니다.
1비트의 가산은 3장의 가산기에서 나타냈습니다. 가산은 이전 음수 표현법에서 중복되는 내용이 많기때문에 예제만 첨부 합니다.

1. 부호와 절대치

2. 부호와 2의 보수

3.부호와 1의 보수

감산
감산을 하는 데는 감산기를 사용하여 직접 감산하는 방법과 감수의 보수를 이용하여 가산기로 감산하는 방법이 있습니다.
직접 감산은 탁상 계산기에, 가산기를 이용한 감산은 일반 전자계산기에 사용됩니다.
직접 감산 회로에는 반감산기와 전감산기가 사용되며 보수 감산 회로에서는 보수기와 가산기가 사용된다. 그리고 2진수로 나타낸 수의 감산은 부호와 절대치로 수를 나타내었을 경우에만 필요하고 2의 보수와 1의 보수에 의해서 나타낸 수의 감산은 감수의 2의 보수 혹은 1의 보수를 취하여 합하면된다. 실제 2진수의 감산은 직접적 감산에 의한 방법보다 보수의 가산을 이용한다. 보수는 주로 2의 보수가많이 사용되고 있습니다.

이진 가 ,감 산기
-2진수의 뺄셈은 2의 보수를 이용한 덧셈으로 계산
-전가산기에 XOR 게이트를 추가하여 덧셈과 뺄셈 연산을 동시수행
M = 0일 때 가산기로 동작
- B⊕0 =B 이므로 전가산기에 원래의 B 값이 입력, 입력캐리에 0입력
-FA 입력은 Ai+Bi 되므로 가산 수행
M =1일 때 감산기로 동작
- B⊕1 =B', C0 =1 이므로 전가산기에는 B에 대한 2의 보수 입력
-FA입력은 Ai+Bi +1이 되므로 감산 수행

승산
부호와 절댓값 형식으로 된 고정 소수점 2진수의 곱셈은 계속적인 시프트와 것셈 연산의 반복으로써 얻어집니다 숫자를 예를 들어 보이면 다음과 같습니다

이는 승수의 연속적인 비트를 낮은 자리수부터 살펴 가는 과정으로 이루어져 있습니다. 승수 비트가 1이면 피승수는 아래로 그대로 써줍니다
그렇지 않으면 0을 아래에 써줍니다. 아래에 연속적인 줄을 이루도록 나열된 숫자들은 앞의 숫자에 대해서 왼쪽으로 한자리씩 이동합니다
마지막으로 보든 숫자가 더해지면 그 합이 승산의 결과인 것입니다.
- 승산의 부호는 승수 와 피승수 의 부호에 의하여 결정됩니다. 부호가 서로 같으면 승산의 부호는 양이며 다르면 음이 됩니다
- 승산의 디지털 컴퓨터에서 수행될 때에는 과정을 약간 변화시키는 것이 편리합니다

제산
제산은 뺄샘의 반복과 시프트(shift)를 사용하는 점에서 승산과 비슷한 방법으로 실행됩니다.

논리 마이크로 연산표
-2개의 2진 변수로 수행될 수 있는 논리 연산은 16가지


조금 깊게 들어가봅시다 응용 부분으로 들어가봅시다
-레지스터 A: 프로세서 레지스터
-레지스터 B: 메모리로 부터 출력된 논리 피연산자
1.selective-set 동작(OR 동작)
레지스터 B의 1에 대응하는 레지스터 A의 비트를 1로 세트
0에 대응하는 부분의 레지스터 A의 비트에는 영향을 주지 않음

2.selective-complement 동작(exclusive -OR 동작 )
레지스터 B의 1에 대응하는 부분의 레지스터 A 의 비트를 보수로 만듭니다.

3. selective-clear 동작 (A<- A^B')
레지스터 B의 1에 대응하는 레지스터 A의 비트를 0으로 클리어합니다
1010 레지스터 A before.
1100 레지스터 B
---------
0010 레지스터 A after
4. mask. 동작(AND 동작)
레지스터 B의 해당하는 레지스터 A의 비트를 0으로 클리어 합니다
1010 레지스터 A before
1100 레지스터 B
---------
1000 레지스터 A after
5. insert 동작
비트 묶음 속에 새로운 값을 삽입하는 동작입니다
원하는 위치 비트의 마스크(AND) 후 원하는 값으로 OR동작
마스크 (mask) 0110 1010 레지스터 A before
0000 1111 레지스터 B
(AND)
--------------
0000 1010 레지스터 A. after masking
삽입(insert) 0000 1010 레지스터 A before
1001 0000 레지스터 B
(OR)
-------------------
1001 1010 레지스터 A after insertion
6. compare 동작 (exclusive -OR 동작)
레지스터 A 와 레지스터 B 를 비교하여 두 개의 워드가 일치하는 A를 0으로 세트
비트 하나하나 비교하는게아니라 비트 통채로 비교 하는겁니다.
1010 레지스터 A before
1011 레지스터 B
---------
0000 레지스터 A after A. <------ A ⊕ B
시프트 마이크로 연산(비트이동 연산)
데이터의 직렬전송을 위하여 사용
논리 연산 및 다른 데이터의 처리동작과 연계되어 사용
직렬 컴퓨터 레지스터 간에 2진 정보를 전송하기 위하여 사용
병렬 컴퓨터에서는 산술, 논리 연산을 수행하기 위하여 사용
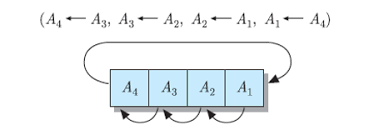
1. 직렬 전송 시프트(SERIAL TANSFER SHIFT) -> 한비트당 하나씩만 이동
- 레지스터 간의 직렬 전송을 하는 시프트
- 좌우 시프트 동작을 기호로 shl과 shr 로 표시
- 좌우 순환 시프트 동작을 cil,cir로 표시
- n은 레지스터의 비트 수를 , Bn은 B의 최우측 셀, A1은 A의 최좌측 셀을 의미
S: shr. A, cir. B, A1. <-- Bn
- 제어 변수 S =1일
-레지스터 B의 끝 비트는 레지스터 A의 첫 비트로 전송
- B를 재저장하기 위해 순환 시프트를 수행
- A는 한 비트씩 오른쪽으로 시프트를 수행
2. 논리 시프트(Logical shift)
논리적인 시프트로서 시프트해서 밀려 나간 비트는 잃어버리며 공백에 새로 들어 오는 비트는 항상 "0" 이 됩니다.
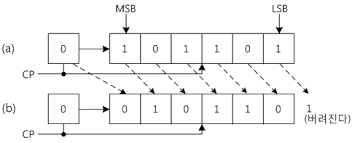
3. 순환 시프트(Circular shift / Rotate)
시프트 레지스터의 양끝의 플립플롭을 연결하여 순환시티느 시프트로 한쪽끝에서 밀려 나간 비트가 다시 반대편에 입력으로 들어오게 됩니다.
4. 산술 시프트(Arithmetic shift )
부호 비트를 포함하여 2진 정보를 시프트하기 위한 마이크로 동작
좌측 시프트(shift left)
시프트에 의해 발생하는 공백에는 "0" 이 삽입
좌측으로 n비트 시프트 하면 원래의 수에 2 ^n을 곱한 것과 같습니다.
우측 시프트(shift right)
시프트에 의해 발생하는 공백에는 "부호 비트" 가 삽입
우측으로 n비트 시프트 하면 원래의 수에 2^n 로 나눈 것과 같습니다.

'CS > 컴퓨터구조' 카테고리의 다른 글
| 제어 장치 (0) | 2023.11.17 |
|---|---|
| 중앙 처리장치(CPU) (0) | 2023.11.10 |
| 음수의 표현 (0) | 2023.10.28 |
| 부동 소수점 2진수 표현 (0) | 2023.10.19 |
| 진법 변환 (0) | 2023.10.19 |



