계산대의 대기열을 떠올리면 쉽게 이해할 수 있는 자료구조입니다.
선형 구조 이며 선입선출(FIFO)의 특성을 갖는 자료구조입니다. 즉 A, B, C, D를 순서대로 삽입하면 꺼낼(삭제) 때도 같은 순서인 A, B, C로 나옵니다. 큐는 스택과 비슷해 보이지만 삽입과 삭제 연산이 같은 쪽이 아니라 서로 다른 쪽에서 일어납니다. 삽입이 일어나는 곳을 후단(rear)라고 하고 삭제가 일어나는 곳을 전단(front)이라고 부릅니다.
큐의 추상 자료형
큐에 저장하는 자료애는 트별한 제한이 없습니다. 연산들도 스택과 유사합니다. 삽입과 삭제가 역시 가장필수적인 연산이고, 공백이나 포화 등의 상태 검사 연산들도 필요합니다. 큐의 추상 자료형은 다금과 같이 정의할 수 있습니다
| 연산 | 설명 |
| init(): | 큐를 초기화 |
| enqueue(e) | 요소 e를 큐의 맨뒤에 삽입합니다 |
| dequeue | 큐의 맨 앞 요소를 삭제하고 반환합니다. |
| is_empty | 큐가 비어있으면 TRUE를 아니면 FALSE를 반환합니다. |
| is_full() | 큐가 가득 차 있으면 TRUE를 아니면 FALSE를 반환합니다 |
| peek() | 큐의 맨 앞 요소를 삭제하지 않고 반환합니다 |

큐에서도 두 가지 오류 상황을 만날 수 있습니다 포화 상태인 큐애 enqueue를 실행하면 오버플로(overflow)가 발상하고 공백상태에서 dequeue나 peek를 실행하면 언더플로(nuderflow) 오류가 발생합니다 따라서 큐를 안정적으로 사용하기 위해서는 이들을 상태의 검사가 필수 적입니다.
큐의 활용
큐는 자료가 들어오는 순서대로 처리하는 구조입니다. 그런대 먼저 들어온 자료를 먼저 처리한다면 그때그때 처리하면 되지만 왜 복잡하게 큐라는 것을 사용하는지 의문입니다. 이것은 자료가 한꺼번에 몰려드는 경우를 생각해 보면 쉽게 이해할 수 있습니다
예를 들어 어떤 음식점에 손님이 별로 없으면 바로바로 서비스할 수 있지만 한꺼번에 몰려오면 모든 테이블이 곽 차면 나머지 손님들을 돌려보낼 수도 있지만 더 좋은 방법은 줄을 세우는 것이 좋을 것입니다
큐는 이처럼 갑자기 데이터가 몰려드는 경우 이들을 잠시 보관할 저장소로 사용합니다 용량이 넉넉한 큐에 데이터를 보관하다가 현재 데이터에 대한 처리가 끝나면 먼저 온 순서대로 하나씩 꺼내 처리하면 어떤 데이터도 버리지 않고 정확히 작업을 마칠 수 있기 때문입니다.
보통 버퍼(buffer)라고 하는데 버퍼링의 개념을 보여주고 있습니다 일상생활에서는 프린터기에 인쇄 버튼을 여러 장 빠르게 처리를 하면 cpu의 처리 속도와 주변장치의 처리 속도의 차이 때문에 데이터가 한 번에 몰려올 수 있기 때문에 그때는 큐를 사용해서 관리합니다
배열을 이용한 큐
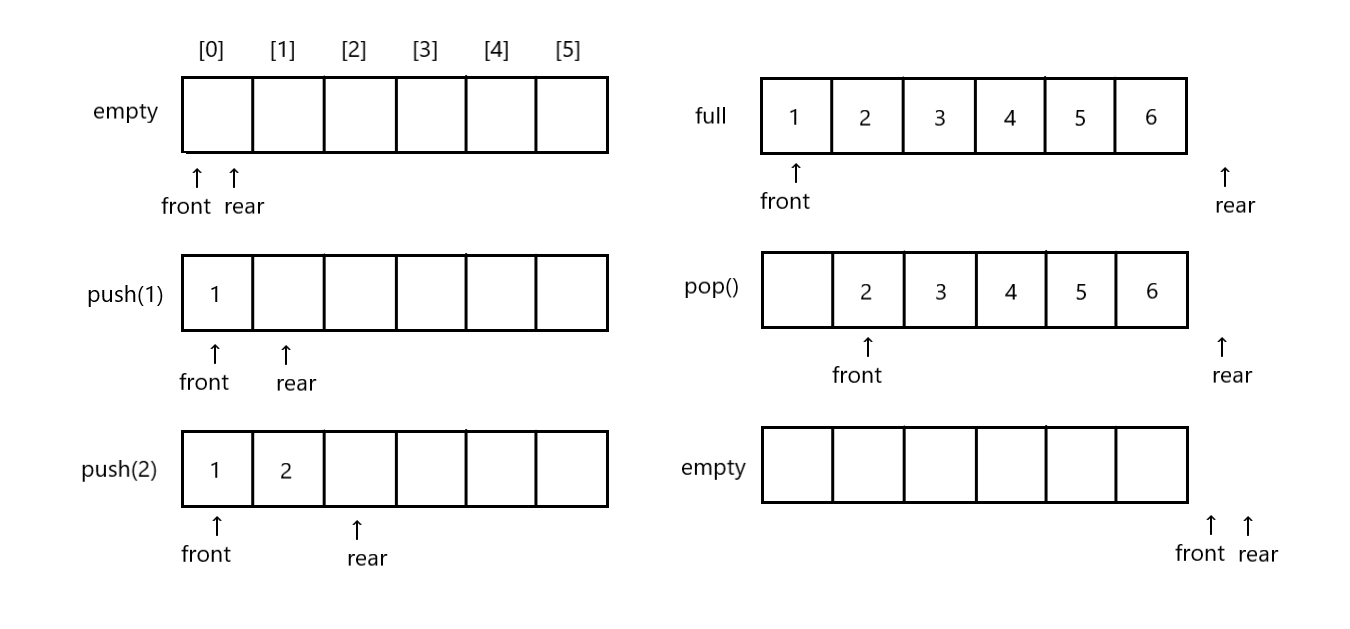
큐도 배열구조와 연결된 구조로 구현할 수 있는데 배열을 이용한 큐의 구조는 이전 그림과 같습니다. 전단과 후단을 모두 사용하므로 스택보다는 약간 더 복잡합니다.

- 요소를 저장할 배열을 data [MAX_SIZE]라 합시다. MAX_SIZE는 큐에 저장할 수 있는 최대 요소의 수입니다
- 전단과 후단을 위한 변수가 필요한데, 이들을 각각 front와 rear라 합시다 rear에는 맨 마지막 요소의 인덱스를 저장하고
front는 큐의 첫 번째 요소가 아니라 그 요소의 바로 앞의 위치를 저장합니다 front의 위치에 유의해야 합니다
큐의 동작
front와 rear의 초깃값은 -1입니다 큐의 1,2,3,4,5 대로 순서대로 삽입(enqueue)될 때마다 rear는 하나씩 증가합니다
삭제(dequeue)할 때는 front를 하나 증가시키고 그 위치의 자료를 꺼냅니다. 이와 같이 동작하는 큐를 선형 큐라고 합니다.
원형 큐
선형 큐의 문제를 깔끔하게 해결할 수 있는 아이디어가 있습니다. 배열을 선형으로 아니라 원형으로 생각하는 것입니다. 이런 큐를 원형 큐라고 합니다. 실제로 배열이 원형인 것은 아니고 인덱스 front와 rear를 원형으로 회전시키는 전략입니다.
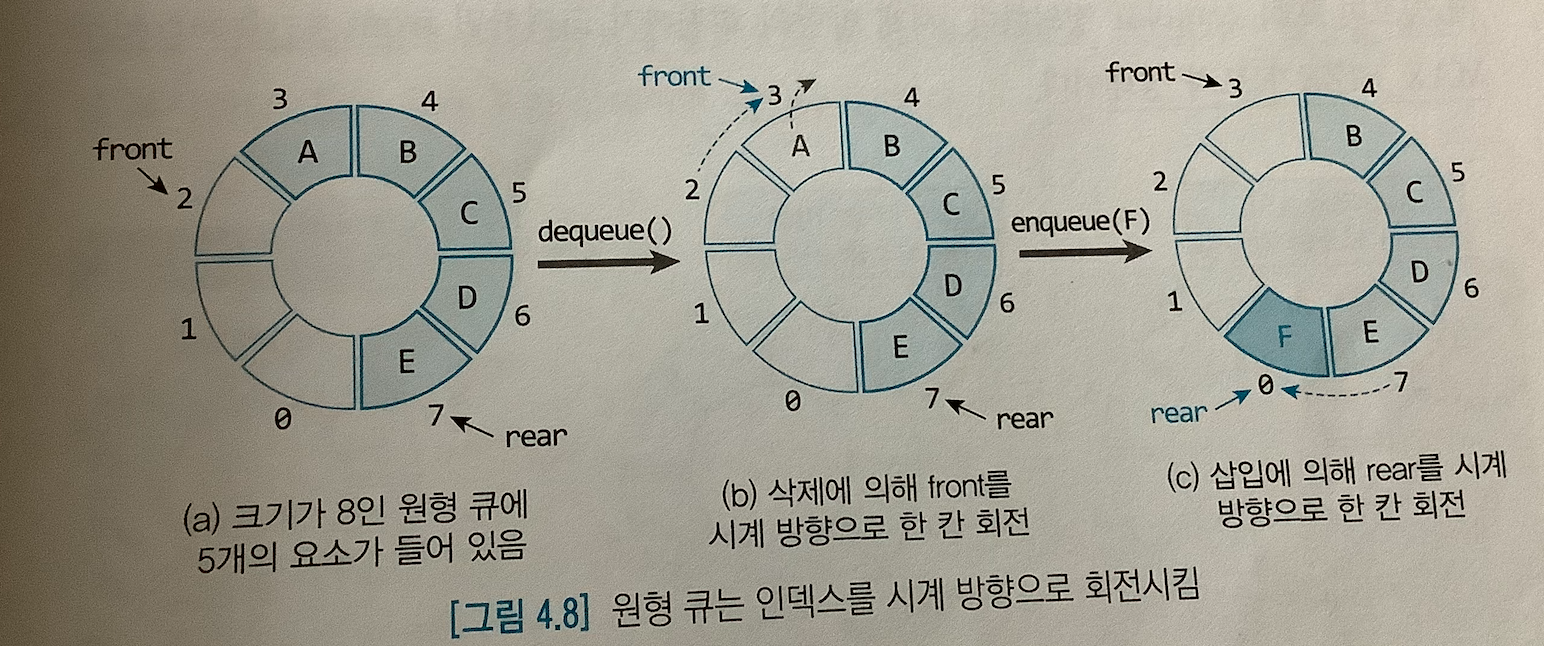
원형 큐의 삭제와 삽입 예를 보여줍니다. rear가 계속 증가하다가 (b)와 같이 배열의 끝에 도달하면 (c)와 같이 다시 0이 됩니다. 따라서 요소 들을 옮길 필요 없이 큐가 공백상태가 아니면 항상 바로 삽입할 수 있습니다. 인덱스의 회전은 삭제를 위한 front도 마찬가지로 적용됩니다.
시계 방향의 회전은 어떻게 처리할 수 있을까? front나 rear가 계속 증가하다가 배열의 크기(MAX_SIZE)와 같아지면 다시 0으로 만들어주면 됩니다. 물론 조건문을 사용할 수도 있지만 나머지 연산(%)을 이용해 간결하게 표현할 수 있습니다
- 전단 회전 :front <- (front+1)% MAX_SIZE
- 후단 회전 :rear <- (rear+1)% MAX_SIZE
이 방법은 회전시킬 때 정말 많이 사용하는 알고리즘으로 알고 있으면 도움이 됩니다.
공백 상태와 포화 상태를 검사하는 is_empty(), is_full()
원형 큐의 공백 상태는 front == rear인 경우입니다. 이들이 0이 되어야 할 필요는 없고 단지 front와 rear가 같은 곳을 가리키기만 하면 큐는 공백 상태입니다
포화상태는 달라집니다. 밑그림 (c)와 같은 상태를 생각하기 쉽지만 문제가 있습니다 (c)는 front==rear인 상태로 공백 상태인 (a)와 구분이 되지 않습니다 따라서 원형 큐에서는 보통 하나의 자리를 비워두는 전략을 사용합니다. 즉 (b)와 같이 front가 rear의 바로 다음에 있으면 포화 상태라고 정의합니다. 시계 방향의 회전까지 고려하면 front == (rear+1)% MAX_SIZE가 포화상태입니다.

덱(deque)
덱(deque)은 double -ended queue의 줄임말입니다 디큐라고 부르는 분들도 있지만 삭제하는 함수도 디큐라 읽기 때문에 구분 짓기 위해서 덱이라고 읽는 것이 맞다고 교수님들이 말씀하시니 우리도 덱으로 읽읍시다 덱은 전단과 후단에서 무도 삽입과 삭제가 가능한 큐를 의미합니다 그렇지만 여전히 중간에 삽입하거나 삭제하는 것은 허용하지 않습니다 덱의 구조는 큐와 거의 같습니다.

덱의 추상 자료형
덱은 큐보다 입출력이 자유로워서 연산도 몇 가지 추가됩니다.
| 연산 | 설명 |
| init | 덱을 초기화 합니다 |
| is_empty() | 덱이 비어 있으면 TRUE를 아니면 FALSE를 반환합니다 |
| is_full() | 덱이 가득차 있으면 TRUE를 아니면 FALSE를 반환합니다 |
| add_front(e) | 맨앞 (전단)에 새로운 요소 e를 추가합니다 |
| delete _front() | 맨앞 (전단)의 요소를 꺼내서 반환합니다 |
| get_front() | 맨 앞 (전단)의 요소를 꺼내지 않고 반환합니다 |
| add_rear(e) | 맨 뒤(후단)에 새로운 요소 e를 추가합니다 |
| delete_rear() | 맨뒤(후단)의 요소를 꺼내서 반환합니다. |
| get_rear() | 맨뒤(후단)의 요소를 꺼내지 않고 반환합니다. |

원형 덱
덱은 큐와 구조가 같으므로 원형 큐와 비슷하게 원형 덱(circular deque)으로 구현하는 것이 좋습니다 이때 주의해야 할 연산은 front와 rear를 감소시켜야 하는 delete_rear()와 add_front()입니다 이들은 enqueue()나 dequeue()와 달리 인덱스를 원형으로 하나씩 줄여야 하는데 , 이것은 반시계 방향의 회전을 의미합니다. 이를 위한 인덱스 처리는 시계 방향과 회전과 비슷하게 나머지 연산을 이용해 간결하게 표현할 수 있습니다.
전단 회전(반시계 방향): front <-(front-1+MAX_SIZE) % MAX_SIZE
후단 회전(반시계 방향): rear <- (rear-1+MAX_SIZE)% MAX_SIZE
예를 들어 밑그림처럼 delete_rear()를 수행하면 rear를 수행하면 rear는 3에서 2로 줄어듭니다 또한, (b)에서 addFront(D)를 수행하면 (c)와 같이 front는 0에서 7(=(0-1+8)%8)로 회전합니다.