지하철 노선이나 SNS 인맥 관계, 최근 딥러닝 분야에서의 복잡한 데이터 흐름 등은 선형 자료구조는 물론이고 트리로도 표현하기 쉽지 않습니다 이들은 모두 다양한 객체들이 서로 복잡하게 연결된 구조를 갖는데 , 그래프는 이런 관계를 표현할 수 있는 훌륭한 논리적 도구입니다. 사실 선형 자료구조나 트리도 그래프로 표현할 수 있으므로 그래프의 한 종류로 볼 수 있고, 따라서 그래프는 가장 일반화된 자료구조입니다.
그래프는 정점(vertex)과 간선(edge)의 집합으로 구성되는데, 그래프 G는 G = (V, E)와 같이 정의됩니다. 이때, V는 정점들의 집합을 , E는 간선들의 집합을 의미합니다. 정점은 객체(object)를 간선은 객체 간의 관계를 표현하는데, 정점 D와 E를 연결하는 간선은 (D, E)와 같이 정점 쌍으로 표현됩니다. 즉 그래프는 오직 정점과 간선의 집합으로 정의됩니다.
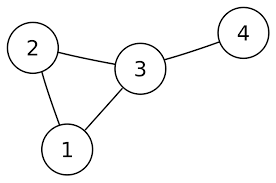
그래프의 종류
무방향 그래프
간선에 방향이 표시되지 않은 그래프를 말합니다 하나의 간선은 양방향으로 갈 수 있는 길을 의미합니다.

노드 :{A, B, C, D, E, F, G, H}.
간선 :{(A, B), (A, C), (C, D)(B, E), (D, E), (E, F), (E, H), (F, G)}
방향 그래프
간선에 방향성이 존재하는 그래프입니다. 일반통행 도로와 같이 한족으로만 갈 수 있습니다. <A, B>로 표시할 때 첫 번째 A가 시작 B가 끝
<B, A>로 표시하면 B가 시작 A 가 끝으로 의미되며 <A, B> <B, A>는 서로 다른 간선입니다.
가중치 그래프
간선에 비용이나 가중치가 할당된 그래프를 말합니다. 네트워크(network)라고 합니다 간선이 정점 사이의 연결 여부뿐만 아니라 연결 강도까지 나타내므로 보다 복잡한 관계를 표현할 수 있습니다. 예를 들어 고속도로거나 이동시간, 통신망의 사용료 등을 추가로 표현할 수 있어 응용분야가 광범위합니다.

부분 그래프
그래프를 구성하는 정점의 집합과 간선의 집합의 부분집합으로 이루어진 그래프를 부분 그래프 라고 합니다.

그래프 용어
- 인접 정점 (adjacent vertex): 간선에 의해 직접 연결된 정점을 말합니다. G1에서 정점 B의 인접 정점은 A와 C입니다.

- 정점의 차수(degree):정점에 연결된 간선의 수를 말합니다. 무방향 그래프에서는 인접한 정점의 수가 차수인데, 예를 들어 G1의 정점 A는 차수가 3입니다. 방향 그래프에서는 차수를 진입차수와 진출 차수로 구분되어야 합니다. 각각 들어오는 간선과 외부로 향하는 간선의 수입니다.
예를 들어 G3의 정점 B는 진입차수가 1 진출 차수가 2입니다
무방향 그래프에서는 모든 정점의 차수가 합이 간선수의 2배이지만, 방향 그래프에서는 진입 차수나 진출 차수의 합이 안선의 수와 같습니다. - 경로(path): 간선을 따라서 갈 수 있는 길입니다 정점(노드)의 나열로 표시됩니다. 그리고 반드시 간선이 있어야 합니다
경로 길이 : 경로를 구성하는 데 사용된 간선의 수 - 단순 경로(simple path)와 사이클(cycle) : 경로 중에서 반복되는 간선이 없는 경로를 단순 경로라 합니다 그리고 단순 경로의 시작 정점과 종료 정점이 같다면 이러한 경로를 사이클이라고 합니다.

- 연결 그래프(connected graph): 모든 정점 사이에 경로가 존재하는 그래프를 말합니다. 따로 떨어진 정점이 없이 모든 정점이 연결되어 있는데 그렇지 않은 그래프는 비연결 그래프라고 합니다
- 트리(Tree): 사이클을 가지지 않는 연결 그래프를 말합니다. 사이클이 없으면 임의의 두 정점을 연결하는 경로는 오직 하나뿐입니다. 두 가지 경로가 존재한다면 이들에 의해 사이클을 형성되기 때문입니다.
- 완전 그래프(complete graph): 모든 정점 간에 간선이 존재하는 그래프를 말합니다. 정점수가 n인 무방향 완전 그래프에서 하나의 정점이 n-1개의 다른 정점으로 연결되므로 전체 간선의 수는 n*((x-1)/2가 됩니다.
그래프의 추상 자료형
| 연산 | 설명 |
| is_empty() | 그래프가 공백 상태인지를 검사한다 |
| insert_vertex(v) | 그래프가 정점 v를 삽입한다 |
| insert_edge(u,v) | 그래프에 간선 (u,v)를 삽입한다 |
| delete_vertex(x) | 정점v를 그래프에서 삭제한다. |
| delete_edge(u,v) | 간선(u,v)를 그래프에서 삭제한다. |
| adjacent(v) | 정점 v의 모든 인접 정점을 반환한다. |
| degree(v) | 정점 v의 차수를 반환한다. |
그래프의 표현
인접 행렬을 이용한 표현
간선의 집합을 2 차원 배열로 표현할 수 있습니다. 이걸 인접 행렬(adjacency matrix)이라 하는데. 행렬의 각 성분이 두 정점의 연결 관계를 나타냅니다. 행렬의 크기는 n*n으로 n은 정점의 수입니다. a에 (1,3)은 간선이 없기 때문에 0으로 표시하고 간선이 있는 것들은 1로 표기합니다.

그래프에서 정점들 사이에는 "순서"가 없습니다. 정점 순서는 편의상 임의로 정한 것일 뿐이며 만약 정점의 나열 순서를 변경한다면 인접 행렬도 달라집니다.
인접 리스트를 이용한 표현
각 정점이 인접한 정점의 리스트를 갖도록 하여 간선들을 표현할 수도 있습니다. 이것을 인접 리스트(adjacency list)라고 합니다.
예를 들어 두 번째 A에서 간선으로 연결된 노드는 2개 이므로 리스트의 길이도 2인 인접 리스트로 표현할 수 있습니다.
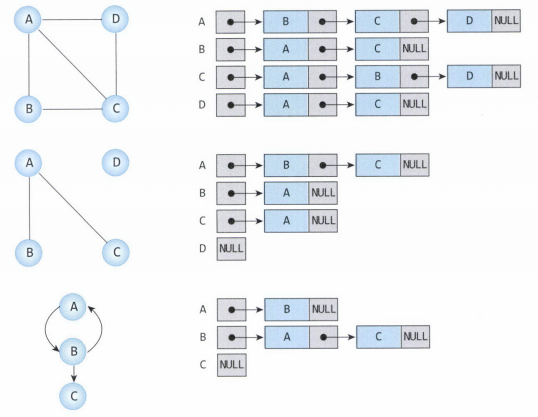
인접 행렬과 인접 리스트 비교
단지 그래프를 표현하기 위해서라면 어느 것을 사용해도 문제가 없습니다. 그렇지만 그래프로 어떤 작업을 하려면 차이가 있습니다. 정점수가 n이고 간선의 수가 e인 무방향 그래프에서 두 표현의 복잡도를 비교해 봅시다.
| 인접 행렬 | 인접 리스트 |
| 간선의 수에 무관하게 항상 n²개의 메모리 공간이 필요합니다 따라서 정점에 비해 간선의 수가 매우 많은 조밀 그래프(dense graph)에서 효과적입니다. | n개의 연결 리스트가 필요하고 2e개의 노드가 필요합니다 즉 n+2e개의 메모리 공간이 필요합니다 따라서 정점에 비해 간선의수가 매우적은 희소 그래프(sparse graph)에서 효과적입니다. |
| u와 v를 연결하는 간선(u,v)의 유무는 인접 행렬의 요소 adj[u][v]를 조사하면 바로 알 수 있습니다. 따라서 O(1)입니다. | (u,v)가 있는지는 u의 연결 리스트 전체를 조사 해야 알수 있습니다. 정점u의 차수를 dᵤ라고 한다면 시간 복잡도는 O(dᵤ)입니다. |
| v의 차수는 인접 행렬에서 v에 해당하는 행의 모든 성분을 조사해야 알 수 있습니다. 따라서 복잡도 는 O(n)입니다. | v의 차수는 v의 연결 리스트의 길이입니다. 따라서 복잡도는 v의 차수에 비례하는 O(dᵤ)입니다. |
| v의 모든 인접 정점을 구하려면 해당 행의 모든 요소를 조사해야 하므로 O(n)의 시간이 요구됩니다. | 정점v의 연결 리스트의 모든 요소를 방문해야 하므로 O(dᵤ)입니다. |
| 그래프의 전체 간선 수를 구하려면 인접 행렬 전체를 조사해야 하므로 O(n²)의 시간이 요구됩니다. | 모든 인접 리스트의 모든 요소를 방문해야 하므로 O(n+e)의 연산이 요구됩니다. |
두 표현 방법은 연산에 따라 약간씩 차이가 있지만 어느 한쪽도 압도적으로 장점이 많지는 않습니다. 따라서 목적에 따라 적절히 결정하는 것이 좋습니다.
그래프 탐색
모든 정점을 한 번씩 방문하는 작업을 말합니다.
깊이 우선 탐색 (BFS)
깊이 우선 탐색(depth first search)은 시작 정점에서부터 임의의 방향으로 갈수 있는 곳까지 깊이를 탐색하다가 더이상 갈 곳이 없으면 가장 마지막에 만났던 갈림길로 되돌아와 다른 방향을 다시 탐색하는 것을 말합니다 탐색은 아직 방문하지 않은 정점에 대해서만 진행하므로 방문한 정점에서는 반드시 방문 표시를 합니다. DFS는 가장 최근에 만났던 갈림길로 되돌아가야 하므로 스택을 사용합니다. 그렇지만 순환을 이용하면 명시적인 스택을 사용하지 않고도 간략하게 기술 할수 있습니다. 정점의 방문 여부를 기록하는 리스트는 맨 처음에 모두 FALSE로 초기화 됩니다.

너비 우선 탐색
너비 우선 탐색(breath first search : BFS) 은 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 탐색 방법 입니다. 이것은 트리의 레벨 순회와 비슷합니다. 가까운 정점들을 차례로 저장하고 들어간 순서대로 꺼낼 수 있는 자료구조 큐를 사용 하고 맨처음 큐에는 시작정점이 들어가고 그다음으로 큐에서 정점을 꺼내고 방문하지 않은 인접한 정점들을 차례로 방문하고 큐에 삽입합니다 이 과정은 큐가 공백 상태가 될 때까지 반복합니다. 너비 우선 탐색은 시작 정점에서 거리가 가까운 순서대로 정점을 탐색합니다. 이때 거리는 그 정점까지의 경로 중 가장 짧은 경로의 길이를 의미합니다.

신장 트리와 최소비용 신장트리
신장트리(spanning tree)란 그래프의 모든 정점을 포함하는 트리입니다. 트리가 되려면 사이클이 없어야 하고, 모든 정점을 연결해야 하므로 n개의 정점을 정확히 n-1개의 간선으로 연결합니다.

최소 비용 신장트리란?
간선에 정점 사이의 길이나 전송 시간, 비용 등을 할당한 가중치 그래프에서 신장트리의 비용을 트리를 구성하는 간선의 가중치 합으로 정의 할수 있습니다.

prim MST 알고리즘
정점1과 정점 2 사이의 최소 간선의 가중치를 저장하는 알고리즘


Kruskal의 MST알고리즘
사이클을 만들지 않는 가장 가중치가 작은 간선n-1개를 순서대로 선택하는 알고리즘


최단 경로 알고리즘
정점 1 과 정점 2를 연결하는 경로 중에서 가중치 합이 최소인 경로를 말합니다.
Dijkstra의 최단 경로 알고리즘
하나의 정점에서 다른 모든 정점까지 최단 경로를 구하는데 무방향 그래프나 방향 그래프에 모두 적용 가능하며 기본 아이디어는 prim의 MST에서 비슷합니다.
Dijkstra 알고리즘은 시작 정점에서부터 다른 모든 정점까지의 최단 경로의 거리를 구한것입니다.


Floyd 최단 경로 알고리즘
Floyd 알고리즘은 모든 정점 사이의 최단 경로를 한꺼번에 찾아줍니다.
플로이드 와셜 알고리즘은 Dynamic Programming을 사용하여 정점 i에서 j로 직접 가는 경로와 중간에 어느 정점을 거쳐 가는 경로를 비교하여 최단경로를 찾습니다.
이 방식으로 모든 정점 쌍에 대한 최단 거리를 구하게 됩니다.
다음은 중간에 노드 집합 {1,2,..., k}에 속한 노드들만 거쳐서 노드 i에서 j까지 가는 최단 경로의 길이를 의미합니다.
𝑑𝑘[𝑖,𝑗]
k= 0인 경우는 중간에 어떤 노드(k)도 거치지 않고 직접 정점 i에서 j까지 가는 경로를 의미하고, 만약 i에서 j까지 가는 경로가 존재하지 않는다면 무한대로 표시합니다.
𝑑0[𝑖,𝑗]={𝑤𝑖𝑗,if (𝑖,𝑗)∈E∞,otherwise.
중간에 노드 집합 {1,2,..., k}에 속한 노드들만 거쳐서 노드 i에서 j까지 가는 최단경로(𝑑𝑘[𝑖,𝑗])는 두가지 경우가 있습니다.
- 노드 k를 지나는 경우 ( 𝑑𝑘−1[𝑖,𝑘]+𝑑𝑘−1[𝑘,𝑗])
- 노드 k를 지나지 않는 경우 (𝑑𝑘−1[𝑖,𝑗])

이중 짧은 경로가 최단 경로가 되며 다음과 같은 순환식을 얻을 수 있습니다.
𝑑𝑘[𝑖,𝑗]=𝑚𝑖𝑛{𝑑𝑘−1[𝑖,𝑗],𝑑𝑘−1[𝑖,𝑘]+𝑑𝑘−1[𝑘,𝑗]}
https://yoongrammer.tistory.com/90
다른 구글 이미지 등등



